Matlab Examples using MDCS

A few examples for Matlab applications using MDCS (prepared using Matlab version R2011b) are illustrated below.

Example application: 2D random walk

Consider the Matlab .m-file myExample_2DRandWalk.m (listed below), which among other things illustrates the use of sliced variables and independent stremas of random numbers for use with parfor-loops.

This example program generates a number of N independent 2D random walks (a single step has steplength 1 and a random direction). Each random walk performs tMax steps. At each step t, the radius of gyration (Rgyr) of walk i is stored in the array Rgyr_t in the entry Rgyr_t(i,t). While the whole data is availabe for further postprocessing, only the average radius of gyration Rgyr_av and the respective standard error Rgyr_sErr for the time steps 1...tMax are computed immediately (below it will also be shown how to store the data in an output file on HERO for further postprocessing).

 
%% FILE:  myExample_2DRandWalk.m
%  BRIEF: illustrate sliced variables and independent streams 
%         of random numbers for use with parfor-loops
%         
%  DEPENDENCIES:
%    singleRandWalk.m   - implements single random walk
%    averageRgyr.m      - computes average radius of gyration
%                         for time steps 1...tMax
%
%  AUTHOR: Oliver Melchert
%  DATE:   2013-06-05
%

N       = 10000;         % number of independent walks
tMax    = 100;           % number of steps in individual walk
Rgyr_t  = zeros(N,tMax); % matrix to hold results: row=radius 
                         % of gyration as fct of time; 
                         % col=independent random walk instances

parfor n=1:N

        % create random number stream seeded by the
        % current value of n; you can obtain a list
        % of all possible random number streams by
        % typing RandStream.list in the command window
        myStream = RandStream('mt19937ar','Seed',n);

        % obtain radius of gyration as fct of time for 
        % different independent random walks (indepence 
        % of RWs is ensured by connsidering different 
        % random number streams for each RW instance)
        Rgyr_t(n,:) = singleRandWalk(myStream,tMax);

end

% compute average Rgyr and its standard error for all steps
[Rgyr_av,Rgyr_sErr] = averageRgyr(Rgyr_t);

  

As liste above, the .m-file depends on the following files:

• singleRandWalk.m, implementing a single random walk, reading:

 
function [Rgyr_t]=singleRandWalk(randStream,tMax)
% Usage:  [Rgyr_t]=singleRandWalk(randStream,tMax)
% Input:
%   randStream - random number stream
%   tMax       - number of steps in random walk
% Output:
%   Rgyr_r     - array holding the radius of gyration
%                for all considered time steps

  x=0.;y=0.; % initial walker position
  Rgyr_t = zeros(tMax,1);
  for t = 1:tMax
    % implement random step
    phi=2.*pi*rand(randStream);
    x = x+cos(phi);
    y = y+sin(phi);
    % record radius of gyration for current time
    Rgyr_t(t)=sqrt(x*x+y*y);
  end
end
  

• averageRgyr.m, which computes the average radius of gyration of the random walks for time steps 1...tMax, reading:

 
function [avList,stdErrList]=averageRgyr(rawDat)
% Usage: [av]=averageRgyr(rawDat)
% Input:
%  rawData   - array of size [N,tMax] where N is the
%              number of independent random walks and
%              tMax is the number of steps taken by an
%              individual walk
% Returns:
%  av         - aveage radius of gyration for the steps

 [Lx,Ly]=size(rawDat);
  avList = zeros(Ly,1);
  stdErrList = zeros(Ly,1);
  for i = 1:Ly
    [av,var,stdErr] = basicStats(rawDat(:,i));
    avList(i) = av;
    stdErrList(i) = stdErr; 
  end
end

function [av,var,stdErr]=basicStats(x)
% usage: [av,var,stdErr]=basicStats(x)
% Input: 
%  x   - list of numbers
% Returns:
%  av  - average 
%  var - variance
%  stdErr - standard error
  av=sum(x)/length(x);
  var=sum((x-av).^2)/(length(x)-1);
  stdErr=sqrt(var/length(x));
end
  

For test purposes one might execute the myExample_2DRandWalk.m directly from within a Matlab session on a local Desktop PC.

Specifying file dependencies

So as to sumbit the respective job to the local HPC system one might assemble the following job submission script, called mySubmitScript_v1.m:

 
sched = findResource('scheduler','Configuration','HERO');

jobRW =...
   batch(...
        sched,...    
        'myExample_2DRandWalk',...
        'matlabpool',2,...
        'FileDependencies',{...
                           'singleRandWalk.m',...
                           'averageRgyr.m'...
                           }...
        );
  

In the above job submission script, all dependent files are listed as FileDependencies. I.e., the .m-files specified therein are copied from your local desktop PC to the HPC system at run time.

Now, from within a Matlab session I navigate to the Folder where the above .m-files are located in and call the job submission script, i.e.:

 
>> cd MATLAB/R2011b/example/myExamples_matlab/RandWalk/
>> mySubmitScript_v1
runtime    = 24:0:0 (default)
memory     = 1500M (default)
diskspace  = 50G (default)
  

before the job is actually submitted, I need to specify my user ID and password, of course. Once the job is successfully submitted, I can check the state of the job via typing jobRW.state. However, if you want to get some more information on the status of your job, you might want to try to log-in on the HPC system and to simply type the command qstat on the commandline. This will yield several details related to your job which you might process further to see on which execution nodes your job runs, why it won't start directly etc. Note that MATLAB provides only a wrapper for the qstat command which in some cases result in a misleading output. E.g., if, for some reason, your job changes to the error-state it might be that MATLAB erroneously reports it to be in the finished-state.

Once the job (really) has finished, i.e.,

 
>> jobRW.state

ans =

finished
  

I might go on and load the results to my desktop computer, giving

 
>> res=load(jobRW);
>> res

res = 

            N: 10000
      Rgyr_av: [100x1 double]
    Rgyr_sErr: [100x1 double]
       Rgyr_t: [10000x100 double]
          ans: 'finished'
          res: [1x1 struct]
         tMax: 100
  

However, note that there are several drawbacks related to the usage of FileDependencies: E.g.,

• each worker gets an own copy of the respective .m-files when the job starts (in particular, workers that participate in the computing process do not share a set of .m-files in a common location),
• the respective .m-files are not available on the HPC system once the job has finished,
• comparatively large input files need to be copied to the HPC system over and over again, if several computations on the same set of input data are performed.

In many cases a different procedure, based on specifying PathDependencies, outlined below in detail, might be recommendend.

Specifying path dependencies

Basically there are two ways to specify path dependencies. You might either specify them in your job submission script or directly in your main MATLAB .m-file. Below, both approaches are illustrated.

Modifying the job submission script

The idea underlying the specification of path dependencies is that there might be MATLAB modules (or sets of data) you want to routinely use over and over again. Then, having these modules available on your local desktop computer and using file dependencies to copy them to the HPC system at run time results in time and memory consuming, unnecessary operations.

As a remedy you might adopt the following two-step procedure:

1. copy the respective modules to the HPC system
2. upon submitting the job from your local desktop pc, indicate by means of the key word pathDependencies where (on HERO) the respective data files can be found.

This eliminates the need to copy the respective files using the fileDependencies statement. An example of how to accomplish this for the random walk example above is given below.

Just for arguments, say, the content of the two module files singleRandWalk.m and averageRgyr.m will not be changed in the near future and you want to use both files on a regular basis when you submit jobs to the HPC cluster. Hence, it would make sense to copy them to the HPC system and to specify within your job submission script where they can be found for use by any execution host. Following the above two steps you might proceed as follows:

1. create a folder where you will copy both files to. To facilitate intuition and to make this as explicit as possible, I created the folder

 /user/fk5/ifp/agcompphys/alxo9476/SIM/MATLAB/R2011b/my_modules/random_walk

and copied both files there, see

 
alxo9476@hero01:~/SIM/MATLAB/R2011b/my_modules/random_walk$ ls
averageRgyr.m  singleRandWalk.m
  

2. Now, it is no more necessary to specify both files as file dependencies as in the example above. Instead, in your job submission file (here called mySumbitScript_v2.m) you might now specify a path depenency (which relates to your filesystem on the HPC system) as follows:

 
sched = findResource('scheduler','Configuration','HERO');

jobRW =...
   batch(...
        sched,...    
        'myExample_2DRandWalk',...
        'matlabpool',2,...
        'PathDependencies',{'/user/fk5/ifp/agcompphys/alxo9476/SIM/MATLAB/R2011b/my_modules/random_walk'}...
        );

This has the benefit that the files will not be copied to the HPC system at run time and that there is only a single copy of those files on the HPC system, which can be used by all execution hosts (so no multiple copies of the same files necessarry as with the use of file dependencies).

Again, from within a Matlab session navigate to the folder where the job submission file and the main file myExample_2DRandWalk.m are located in and call the job submission script. For me, this reads:

 
>> cd MATLAB/R2011b/example/myExamples_matlab/RandWalk/
>> mySubmitScript_v2
runtime    = 24:0:0 (default)
memory     = 1500M (default)
diskspace  = 50G (default)
  

again, before the job is actually submitted, I need to specify my user ID and password (since I started a new MATLAB session in between). Once the job has finished I might go on and load the results to my desktop computer, giving

 
>> res=load(jobRW);
>> res

res = 

            N: 10000
      Rgyr_av: [100x1 double]
    Rgyr_sErr: [100x1 double]
       Rgyr_t: [10000x100 double]
          ans: 'finished'
          res: [1x1 struct]
         tMax: 100
  

Modifying the main m-file

As an alternative to the above procedure, you might add the folder

 /user/fk5/ifp/agcompphys/alxo9476/SIM/MATLAB/R2011b/my_modules/

to your local MATLAB path by adding the single line

 addpath(genpath('/user/fk5/ifp/agcompphys/alxo9476/SIM/MATLAB/R2011b/my_modules/'));

to the very beginning of the file myExample_2DRandWalk.m. For completeness, note that this adds the above folder my_modules and all its subfolders to your MATLAB path. Consequently, all the m-files contained therein will be available to the execution nodes which contribute to a MATLAB session.

In this case, a proper job submission script (mySubmitScript_v3.m) reads simply:

 
sched = findResource('scheduler','Configuration','HERO');

jobRW =...
   batch(...
        sched,...    
        'myExample_2DRandWalk',...
        'matlabpool',2...
        );
  

As a personal comment, note that, from a point of view of submitting a job to the HPC System, I would always prefer the explicit way of stating path dependencies in the job submission file over the implicit way of indirectly implying them using a modification of the main m-file. The latter choice seems much more vulnerable to later changes!

Storing data on HERO

Consider a situation where your application produces lots of data you want to store for further postprocessing. Often, in particular when you produce lots of data, you also don't want the data to be copied back to your desktop computer, immediately. Instead you might want to store the data on HERO and perhaps mount your HPC-homedirectory later to relocate the data (or the like). Note that, as a default HERO user, you have 110GB of disk space available under your home directory. Below it is illustrated, by means of the random walk example introduced earlier, how to store output data on the HPC system.

The only thing you need to do is to specify a path within your main m-file under which the data should be stored. Therefore you first have to create the corresponding sequence of folders if they do not exist already. To facilitate intuition: in my case I decided to store the data under the path

 /user/fk5/ifp/agcompphys/alxo9476/SIM/MATLAB/R2011b/my_data/random_walk/

I created the folder my_data/rand_walk/ for that purpose. Right now, the folder is empty.

In the main file (here called myExample_2DRandWalk_saveData.m) I implemented the following changes:

 
N       = 10000;         % number of independent walks
tMax    = 100;           % number of steps in individual walk
Rgyr_t  = zeros(N,tMax); % matrix to hold results: row=radius 
                         % of gyration as fct of time; 
                         % col=independent random walk instances

% absolute path to file on HERO where data will be saved 
outFileName=sprintf('/user/fk5/ifp/agcompphys/alxo9476/SIM/MATLAB/R2011b/my_data/random_walk/rw2d_N%d_t%d.dat',N,tMax);

parfor n=1:N

        % create random number stream seeded by the
        % current value of n; you can obtain a list
        % of all possible random number streams by
        % typing RandStream.list in the command window
        myStream = RandStream('mt19937ar','Seed',n);

        % obtain radius of gyration as fct of time for 
        % different independent random walks (indepence 
        % of RWs is ensured by connsidering different 
        % random number streams for each RW instance)
        Rgyr_t(n,:) = singleRandWalk(myStream,tMax);

end

% compute average Rgyr and its standard error for all steps
[Rgyr_av,Rgyr_sErr] = averageRgyr(Rgyr_t);

% write data to output file on HERO
saveData_Rgyr(outFileName,Rgyr_av, Rgyr_sErr);
  

Note that the outFileName is specified directly in the main m-file (there are also more elegant ways to accomplish this, however, for the moment this will do!) and the new function, termed saveData_Rgyr is called. The latter function will just write out some statistical summary measures related to the gyration radii of the 2D random walks. For completeness, it reads:

 
function saveData(fileName,Rgyr_av,Rgyr_sErr)
% Usage: saveData(fileName,myData)
% Input:
%  fileName - name of output file
%  myData   - data to be saved in file
% Returns:      nothing
  outFile  = fopen(fileName,'w');
  fprintf(outFile,'# t Rgyr_av Rgyr_sErr \n');
  for i = 1:length(Rgyr_av)
    fprintf(outFile,'%d %f %f\n',i,Rgyr_av(i),Rgyr_sErr(i));
  end
  fclose(outFile);
end
  

Now, say, my opinion on the proper output format is not settled yet and I consider to experiment with different kinds of output formatting styles, for that matter. Then it is completely fine to specify some of the dependent files as path dependencies (namely those that are unlikely to change soon) and others as file dependencies (namely those which are under development). Here, joining in the specification of path dependencies within a job submission script, a proper submission script (here called mySubmitScript_v5.m) might read:

 
sched = findResource('scheduler','Configuration','HERO');

jobRW =...
   batch(...
        sched,...    
        'myExample_2DRandWalk_saveData',...
        'matlabpool',2,...
        'FileDependencies',{'saveData_Rgyr.m'},...
        'PathDependencies',{'/user/fk5/ifp/agcompphys/alxo9476/SIM/MATLAB/R2011b/my_modules/random_walk'}...
        );
  

Again, starting a MATLAB session, changing to the directory where the myExample_2DRandWalk_saveData.m and saveData_Rgyr.m files are located in, launching the submission script mySubmitScript_v5.m and waiting for the job to finish, i.e.

 
>> cd MATLAB/R2011b/example/myExamples_matlab/RandWalk/
>> mySubmitScript_v5
runtime    = 24:0:0 (default)
memory     = 1500M (default)
diskspace  = 50G (default)
>> jobRW.state

ans =

finished
  

Once the job is done, the output file rw2d_N10000_t100.dat (as specified in the main script myExample_2DRandWalk_saveData.m) is created in the folder under the path

 /user/fk5/ifp/agcompphys/alxo9476/SIM/MATLAB/R2011b/my_data/random_walk/

which contains the output data in the format as implemented by the function saveData_Rgyr.m, i.e.

 
alxo9476@hero01:~/SIM/MATLAB/R2011b/my_data/random_walk$ head rw2d_N10000_t100.dat 
# t Rgyr_av Rgyr_sErr 
1 1.000000 0.000000
2 1.273834 0.006120
3 1.572438 0.007235
4 1.795441 0.008645
5 1.998900 0.009714
6 2.168326 0.010867
7 2.355482 0.011766
8 2.519637 0.012721
9 2.683048 0.013456
  

Again, after the job has finished, the respective file remains on HERO and is available for further postprocessing. It is not automatically copied to your local desktop computer.

Postprocessing of the simulated data

Just for completeness a brief analysis and display of the 2D random walk data is presenter here. Once the job has finished and the resulting data is loaded to the desktop computer via res=load(jobRW); its possible to postprocess and display some of the results via the m-file finalPlot.m which reads:

 
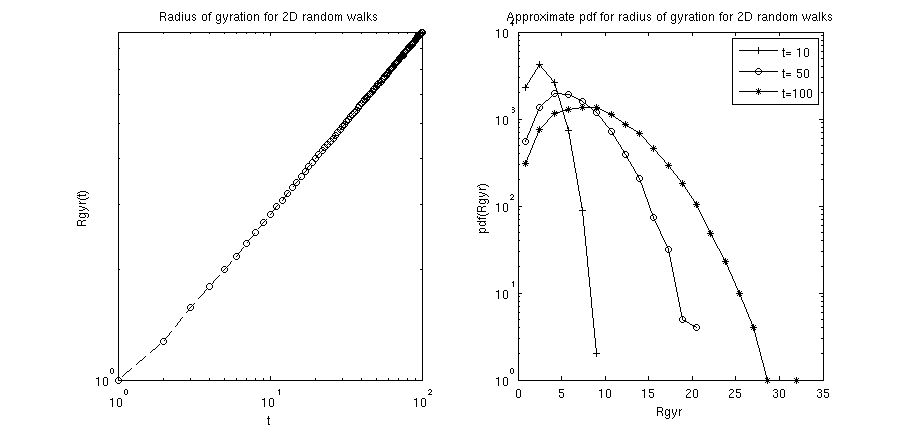
function finalPlot(res)
% Usage: finalPlot(res) 
% Input:
%  res   - simulation results for 2D rand walks 
% Returns: (none)
%
  subplot(1,2,1), plotHelper(res);
  subplot(1,2,2), histHelper(res);
end

function plotHelper(res)
% Usage: plotHelper(res) 
%
% implements plot of the gyration radius as
% function of the walk length 
%
% Input:
%  res   - simulation results for 2D rand walks 
% Returns: (none)
%
  xRange=1:1:100;
  loglog(xRange,res.Rgyr_av,'--ko');
  title('Radius of gyration for 2D random walks');
  xlabel('t');
  ylabel('Rgyr(t)');
end

function histHelper(res)
% Usage: histHelper(res) 
%
% implements histogram of the pdf for gyration 
% radii at chosen times steps 
% of the walk length 
%
% Input:
%  res   - simulation results for 2D rand walks 
% Returns: (none)
%
  set(0,'DefaultAxesColorOrder',[0 0 0],...
        'DefaultAxesLineStyleOrder','-+|-o|-*');
  tList=[10,50,100];
  [events,key]=hist(res.Rgyr_t(:,tList),20);
  semilogy(key,events);
  title('Approximate pdf for radius of gyration for 2D random walks');
  xlabel('Rgyr');
  ylabel('pdf(Rgyr)');
  key = legend('t= 10','t= 50','t=100');
end

Therein, the main function calls two subfunctions:

• plotHelper(res): implements the gyration radius of the 2D random walks as a function of the number of steps in the walk (i.e. the elapsed time since the walk started). The radius of gyration of such an unhindered 2D random walks generally scales $R_{{\rm {gyr}},t}\propto t^{2}$ (for not too short times $t$).
• histHelper(res): implements histograms of the probability density function (pdf) for the gyration radii at specified time steps. In the above example the time steps $t=10,~50$ and $100$ where chosen. For not too short times, one can expect that the pdf is properly characterized by the Rayleigh distribution $p(R_{{\rm {gyr}},t})={\frac {R_{{\rm {gyr}},t}}{\sigma }}\exp {-R_{{\rm {gyr}},t}^{2}/(2\sigma ^{2})}$.

Calling the m-file should yield a figure similar to the following: