Gaussian 2016

Introduction

Gaussian is a computer program for computational chemistry initially released in 1970 by John Pople and his research group at Carnegie Mellon University as Gaussian 70. It has been continuously updated since then. The name originates from Pople's use of Gaussian orbitals to speed up calculations compared to those using Slater-type orbitals, a choice made to improve performance on the limited computing capacities of then-current computer hardware for Hartree–Fock calculations.

Installed version

The currently installed version of Gaussian is 09 Rev D.01.

Available abilities

According to the official homepage, Gaussian 09 Rev. D01 has the following abilities:

• Molecular mechanics
  • AMBER
  • Universal force field (UFF)
  • Dreiding force field
• Semi-empirical quantum chemistry method calculations
  • Austin Model 1 (AM1), PM3, CNDO, INDO, MINDO/3, MNDO
• Self-consistent field (SCF methods)
  • Hartree–Fock method: restricted, unrestricted, and restricted open-shell.
• Møller–Plesset perturbation theory (MP2, MP3, MP4, MP5).
• Built-in density functional theory (DFT) methods
  • B3LYP and other hybrid functionals
  • Exchange functionals: PBE, MPW, PW91, Slater, X-alpha, Gill96, TPSS.
  • Correlation functionals: PBE, TPSS, VWN, PW91, LYP, PL, P86, B95
• ONIOM (QM/MM method) up to three layers
• Complete active space (CAS) and multi-configurational self-consistent field calculations
• Coupled cluster calculations
• Quadratic configuration interaction (QCI) methods
• Quantum chemistry composite methods (CBS-QB3, CBS-4, CBS-Q, CBS-Q/APNO, G1, G2, G3, W1 high-accuracy methods)

Using Gaussian 09.D01 on the HPC cluster

If you want to find out more about Gaussian on the HPC cluster, you can use the command

 module spider gaussian

which will give you an output looking like this

----- /cm/shared/uniol/modulefiles/chem -----
... gaussian/g09.b01 ...

To load a specific version of Gaussian use the full name of the module, e.g. to load Rev. D.01:

[abcd1234@hpcl001]$ module load gaussian/g09.d01
[abcd1234@hpcl001]$ module list
Currently loaded modules: ... gaussian/g09.d01 ...

Linda Jobs

Note: Rev. D.01 has a bug that can cause Gaussian jobs to fail during geometry optimization. See below (or click here) for details and possible work-arounds.

Optimizing the runtime of your jobs

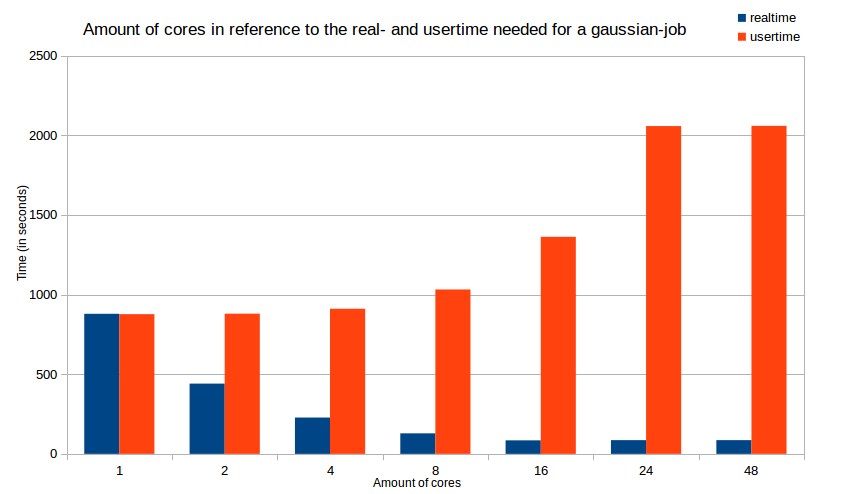
Optimizing the runtime of your jobs will not only safe your time, it will also safe resources (cores, memory, time etc.) for everyone else using the cluster. Therefore you should determine the best amount of cores for your particular job. The following diagramm will show the time difference (splitted into real time and user time) in terms of the amount of used cores.

g09run's new feature

If you've used Gaussian 09.D01 on the old cluster, you will already know what the command g09run in your jobscript does: its runs Gaussian with the given inputfile. This remains unchanged on the new cluster. The new feature is simple, but very effective for saving resources that would otherwise be "wasted":

We've implemented the possibility to add another option beside naming the inputfile to g09run.

Current issues with Gaussian 09 Rev. D.01

Currently Rev. D.01 has a bug which can cause geometry optimizations to fail. If this happens, the following error message will appear in your log- or out-file:

 Operation on file out of range.
  FileIO: IOper= 1 IFilNo(1)=  -526 Len=      784996 IPos=           0
  Q=   46912509105480
  ....
 Error termination in NtrErr:
 NtrErr Called from FileIO.

The explanation from Gaussian's technical support:

This problem appears in cases where one ends up with different orthonormal subsets of basis functions at different geometries. The "Operation on file out of range" message appears right after the program tries to do an interpolation of two SCF solutions when generating the initial orbital guess for the current geometry optimization point. The goal here is to generate an improved guess for the current point but it failed. The interpolation of the previous two SCF solutions to generate the new initial guess was a new feature introduced in G09 rev. D.01. The reason why this failed in this particular case is because the total number of independent basis functions is different between the two sets of orbitals. We will have this bug fixed in a future Gaussian release, so the guess interpolation works even if the number of independent basis functions is different.

There a number of suggestions from the technical support on how to work around this problem:

A) Use “Guess=Always” to turn off this guess interpolation feature. Option "A" would work in many cases, although it may not be a viable alternative in cases where the desired SCF solution is difficult to get from the default guess and one has to prepare a special initial guess. You may try this for your case.

B) Just start a new geometry optimization from that final point reading the geometry from the checkpoint file. Option "B" should work just fine although you may run into the same issue again if, after a few geometry optimization steps, one ends up again in the scenario of having two geometries with two different numbers of basis functions.

C) Lower the threshold for selecting the linearly independent set by one order of magnitude, which may result in keeping all functions. The aforementioned threshold is controlled by "IOp(3/59=N)" which sets the threshold to 1.0D-N (N=6 is the default). Note that because an IOp is being used, one would need to run the optimization and frequency calculations separately and not as a compound job ("Opt Freq"), because IOps are not passed down to compound jobs. You may also want to use “Integral=(Acc2E=11)” or “Integral=(Acc2E=12)” if you lower this threshold as the calculations may not be as numerically robust as with the default thresholds. Option "C" may work well in many cases where there is only one (or very few) eigenvalue of the overlap matrix that is near the threshold for linear dependencies, so it may just work fine to use "IOp(3/59=7)", which will be keeping all the functions. Because of this situation, and because of potential convergence issues derived from including functions that are nearly linearly dependent, I strongly recommend using a better integral accuracy than the default, for example "Integral=(Acc2E=12)", which is two orders of magnitude better than default.

D) Use fewer diffuse functions or a better balanced basis set, so there aren’t linear dependencies with the default threshold and thus no functions are dropped. Option "D" is good since it would avoid issues with linear dependencies altogether, although it has the disadvantage that you would not be able to reproduce other results with the basis set that you are using.

Documentation

For further informations, visit the official homepage of Gaussian.